As Cloud Economists, we’re often asked when it makes sense for an object to be in Amazon S3’s Intelligent-Tiering (“S3-IT”) storage class. The answer, as is unfortunately often the case in the world of consulting, is “it depends”.
There are two primary considerations before you jump into S3-IT: an object’s access pattern and its size.
S3-IT and object access patterns
S3-IT is an extremely handy way to make sure your objects are stored in the appropriate storage tier without having to write complicated lifecycle management policies or incur the cost of lifecycle transitions and minimum retention periods. Maintaining lifecycle management policies and making thoughtful choices about object tiering both require engineer time, which is a lot more expensive than the $0.0025 per 1,000 objects monthly management fee. For this reason, our Cloud Economists often recommend that clients treat S3-IT as the default unless their objects’ access patterns are extremely well-understood. In many cases, it’s cheaper to just let S3-IT figure out where to put your object.
There’s one additional S3-IT caveat customers should be aware of. The S3 Standard storage class is designed for 99.99% availability, while S3 Intelligent-Tiering loses a 9 from the end of that target to offer only 99.9% availability. At large scale, you’ll indeed start to see object retrieval failures more frequently on tiers other than S3 Standard.
S3-IT and object size
Since S3-IT is a good default option for most objects’ access patterns, let’s take that off the table and only look at the monthly storage component of the object’s total cost of ownership (TCO). How big does an object need to be in order for S3-IT to make more sense than the Standard tier from a storage cost perspective?
To come up with a concrete answer to this question, let’s make the simplifying assumption that an object is written once and never read or re-written thereafter. Let’s also make the simplifying assumption that a month is 30 days long, so we don’t have to do fractional math to compute the average cost of an object in GiB-days.
So, to calculate the TCO of this hypothetical object, we have to model the object’s movement through S3-IT’s various tiers over time.
In all different flavors of Intelligent-Tiering, a new object’s first three months of existence are the same: It spends the first month in the Frequent tier and the next two months in the Infrequent Access tier. Where it spends the rest of its existence depends on whether S3-IT’s Deep Archive or Archive tiers are enabled for that object. Therefore, there are three flavors of S3-IT to consider:
- “Vanilla” S3-IT: If neither Deep Archive nor Archive are enabled, the object spends the rest of its existence in the Archive Instant tier. This is the default option.
- S3-IT + Deep Archive: If only Deep Archive is enabled, the object spends three months in the Archive Instant tier and all subsequent months in the Deep Archive tier.
- S3-IT + Archive + Deep Archive: If both Archive and Deep Archive tiers are enabled, the object spends three months in the Archive tier and the rest in the Deep Archive tier.
To make things even more complicated, S3-IT tiers tack on an additional management overhead fee per object-month, and the Archive and Deep Archive tiers store some additional metadata that you also pay for: 8 KiB for the name of the object (billed at Standard tier rates) and 32 KiB for “index and related metadata” (stored at the Glacier and Glacier Deep Archive rates, respectively).
If we think back to high school math class, it sounds like storage cost in S3-IT as a function of time is a piecewise-linear function. Luckily for us, cost of ownership over a given fixed period of time is a linear function of object size.
Calculating S3-IT costs
Since cost of ownership over a fixed period of time is a linear function, we can describe the relationship between object size (x) and storage cost (y) over a fixed period like this:
y_1 is how much it costs to store x_1 bytes for the given time period, and m is the marginal cost of storing an additional byte for that same time period.
Calculating S3 Standard costs
We also know that storage cost in the Standard tier is a linear function of object size, but it’s much simpler:
C is the cost per GiB-month of Standard storage in a given region multiplied by the length of the time period in months.
Calculating the Break-Even Point
So far, we have two equations that can tell us how much it costs to store an X KiB object for a given duration in both S3-IT and Standard. The “break-even point” for a given storage duration is the intersection between those two equations, or the value of x for which:
We can solve the above equation for x, which yields:
For object sizes greater than that intersection point, it’s cheaper to store the object in S3-IT. For object sizes less than that point, it’s cheaper to store the object in Standard. Intuitively, the longer you store an object of a given size, the more benefits you accrue from S3-IT and the lower that break-even point should be. The plot below shows that break-even point for storage durations from one year to 20 years[1].
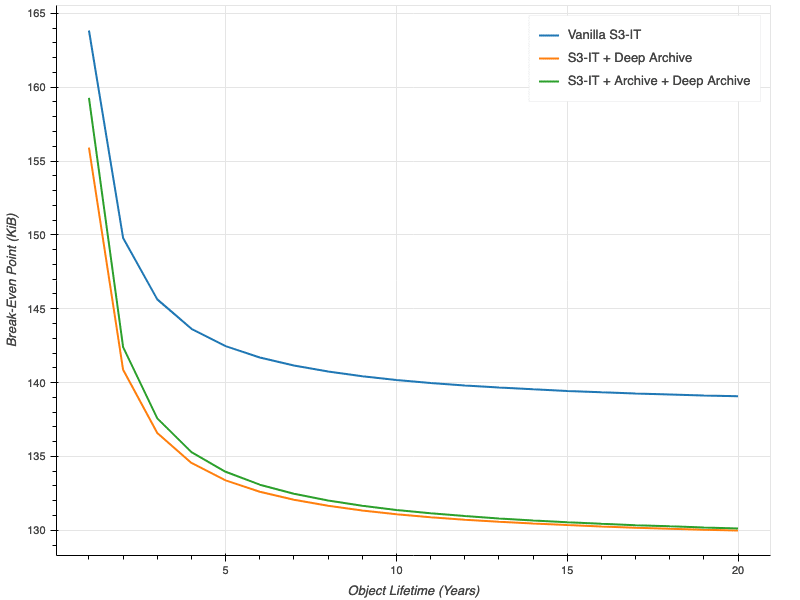
As you can see, for all three flavors of S3-IT, the break-even point starts to level off once the object’s lifetime surpasses about 10 years. The break-even point for S3-IT with colder tiers available is a little lower because the savings in storage costs in those colder tiers add up over time. In all cases, though, the object size at which your break even is very close to the 128 KiB minimum size, regardless of how long you store the object for.
S3-IT has come a long way since its introduction in 2018. At this point, it’s a good default option for most objects under most workloads. One big drawback to adopting S3-IT is that moving objects from other tiers into S3-IT is expensive: it costs $0.01 to transition 1,000 objects, which can add up quickly if you’ve got a lot of objects to transition. However, new objects created in the S3-IT tier aren’t subject to that transition fee, so adopting S3-IT for new workloads won’t cost you anything.
[1] Because this sort of thing can get complicated, it’s worth clarifying that these equations are a function of x (object size) and also implicitly of T (storage duration in months). Solving the equation for the breakeven point is calcuating the breakeven point for a single value of T, and the plot that follows is a plot of that intersection over many values of T, not a plot of y=f(x).


